|
OvergangskurveEn overgangskurve er som ordet sier, en kurver som skaper en overgang, og da mellom en kurveradius til en annen. Den ene kurveradien kan være uendelig, dvs. rett linje. Poenget med en overgangskurve er at toget skal bevege seg jevnt inn i kurven, og ikke kaste seg over fra rett linje til en skarp kurve, slik det ofte er på et MJ-anlegg. Seksjonsskinner med faste radier gir ikke mulgihet for overgangskurve, så dette må utføres med fleksible skinner eller selvbygget spor. Teori
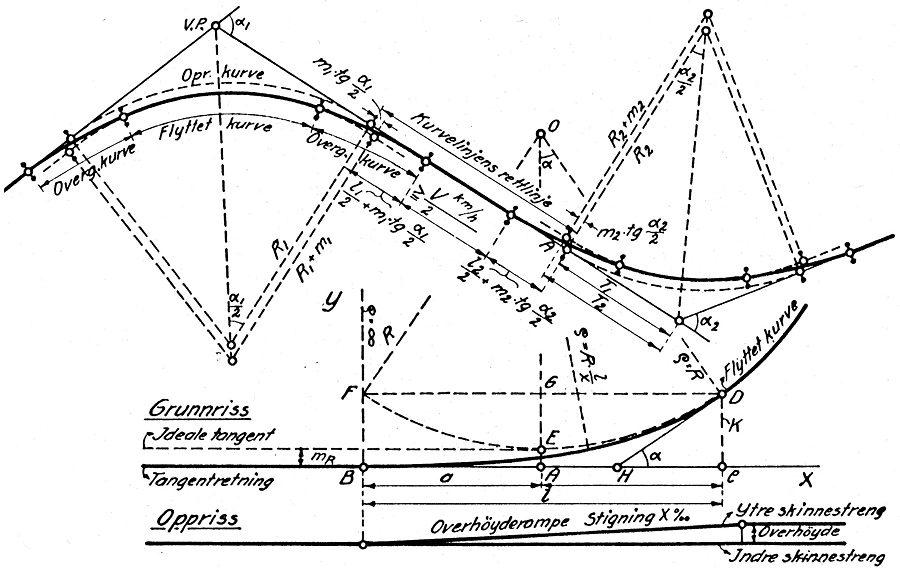
Tegningen er hentet fra prof. Kolbjørn Hejes Vei og jernbanebygging fra 1942, som var lærebok for NTH-studenter i vei og jernbaneteknikk. Den viser hvordan overgangskurven som går mellom punktene B og D på den nederste skissen tangerer rettlinjen i B og den faste radien i D. Den ideelle overgangskurven følger formelen y=x3/6RL, der R er kurvens radius og L er overgangskurvens lengde (l på tegningen). Skissen øverst viser hvordan man legger inn overgangskurver i forhold til et utgangspunkt der kurver med fast radier går rett over i en rettlinje. Man flytter rett og slett kurven litt inn (tilsvarer avstanden AE på skissen nederst) Overgangskurver tar egentlig ikke så stor plass. I H0 vil L kunne være på omtrent 50 cm, dvs. at man trenger et rettstykke på minst 25 cm for å nå punktet B der overgangskurven slutter. Avstanden AE kan være 1 - 1,5 cm i H0. Har man ikke plass til 50 cm overgangskurve, kan man redusere den, men da bør AE også reduseres tilsvarende. Man må prøve seg litt fram når det gjelder forholdet mellom L og AE, så sluttresultatet ser naturlig og jevnt ut. Forenklet praksis på MJ-anleggetHvis man vil det og har tilgang på passende utstyr, kan man selvsagt få plottet en kurve etter formelen y=x3/6RL. Det er imidlertid ikke nødvendig å gjøre det så perfekt. I praksis holder det lenge med å benytte en homogen list som man spenner opp mellom rettlinjen og den faste kurven, og trekke opp overgangskurven med lista som linjal. Bildene nedenfor viser denne prosessen trinn for trinn.
This article is shown 25158 times |
|||||
| Ett tilfeldig blant 30 MJ-bilder fra anlegg jeg sammen med andre eller alene har vært med på å bygge: | ||||||
 | ||||||
I dag 543 treff på mj, og 3167720 totalt siden 28.11.2007 21:52. Dagsgjennomsnitt: 529 treff ·
|
© Svein Sando - e-mail: ssando |
| Start page (Eng.) · Startside (Norw.) · · Display modes: Standard · Without menus: Arial · Times · Times spacious · Large · |
The content of this webpage is subject to Norwegian legislation about copyright, which gives the author all publications wrights. Any further publication of this text and its pictures, completely or partly, can only be done after being authorized to do so by the author. Shorter citation in papers, students essays and so forth can be done if referring to the source. APA style reference to this webpage:
Sando, S. (2012). Overgangskurve. Downloaded 25.04.2024 from https://www.sando.co/index.php?vis=327&nid=3&eng=1
Php-versjon 7.4.33